保研机试训练Day-10

图论DFS

AcWing842. 排列数字

给定一个整数 n，将数字 1∼n 排成一排，将会有很多种排列方法。

现在，请你按照字典序将所有的排列方法输出。

#include<iostream>
using namespace std;

const int N = 10;

int n;
int path[N];
bool st[N];
void dfs(int u){
    if(u == n){
        for(int i=0;i<n;i++) cout << path[i]  << " ";
        cout << endl;
        return;
    }
  
    for(int i=1;i<=n;i++){
        if(!st[i]){
            path[u] = i;
            st[i] = true;
            dfs(u + 1);
            st[i] = false;
        }
    }
}
int main(){
    cin>>n;
    dfs(0);
  
    return 0;
}

AcWing843. n-皇后问题

n−皇后问题是指将 n 个皇后放在 n×n 的国际象棋棋盘上，使得皇后不能相互攻击到，即任意两个皇后都不能处于同一行、同一列或同一斜线上。

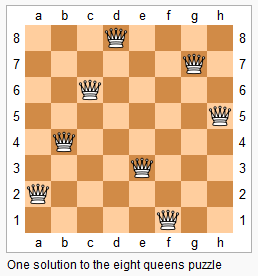
现在给定整数 n，请你输出所有的满足条件的棋子摆法。

搜索顺序1

#include<iostream>
using namespace std;

const int N = 20;

int n;
char g[N][N];
bool col[N], dg[N], udg[N];
void dfs(int u){
    if(u == n){
        for(int i=0;i<n;i++) puts(g[i]);
        puts("");
        return;
    }
  
    for(int i=0;i<n;i++){
        if(!col[i] && !dg[u + i] && !udg[n - u + i]){
            g[u][i] = 'Q';
            col[i] = dg[u + i] =  udg[n - u + i] = true;
            dfs(u + 1);
            col[i] = dg[u + i] =  udg[n - u + i] = false;
            g[u][i] = '.';
        }
    }
}
int main(){
    cin>>n;
    for(int i=0;i<n;i++){
        for(int j=0;j<n;j++){
            g[i][j] = '.';
        }
    }
    dfs(0);
  
    return 0;
}

搜索顺序2

#include<iostream>
using namespace std;

const int N = 20;

int n;
char g[N][N];
bool row[N], col[N], dg[N], udg[N];
void dfs(int u){
    if(u == n){
        for(int i=0;i<n;i++) puts(g[i]);
        puts("");
        return;
    }
  
    for(int i=0;i<n;i++){
        if(!col[i] && !dg[u + i] && !udg[n - u + i]){
            g[u][i] = 'Q';
            col[i] = dg[u + i] =  udg[n - u + i] = true;
            dfs(u + 1);
            col[i] = dg[u + i] =  udg[n - u + i] = false;
            g[u][i] = '.';
        }
    }
}

void dfs1(int x,int y,int s){
    if(y == n){
        y=0;x++;
    }
    if(x==n){
        if(s==n){
            for(int i=0;i<n;i++) puts(g[i]);
            puts("");
        }
        return;
    }
  
    // 不放
    dfs1(x,y+1,s);
  
    // 放
    if(!row[x] && !col[y] && !dg[x+y] && !udg[x-y+n]){
        g[x][y] = 'Q';
        row[x] = col[y] = dg[x+y] = udg[x-y+n] = true;
        dfs1(x,y+1,s+1);
        row[x] = col[y] = dg[x+y] = udg[x-y+n] = false;
        g[x][y] = '.';
    }
}
int main(){
    cin>>n;
    for(int i=0;i<n;i++){
        for(int j=0;j<n;j++){
            g[i][j] = '.';
        }
    }
    // dfs(0);
    dfs1(0,0,0);
    return 0;
}

图论BFS

AcWing844. 走迷宫

给定一个 n×m 的二维整数数组，用来表示一个迷宫，数组中只包含 0 或 1，其中 0 表示可以走的路，1 表示不可通过的墙壁。

最初，有一个人位于左上角 (1,1) 处，已知该人每次可以向上、下、左、右任意一个方向移动一个位置。

请问，该人从左上角移动至右下角 (n,m) 处，至少需要移动多少次。

数据保证 (1,1) 处和 (n,m) 处的数字为 0，且一定至少存在一条通路。

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;

typedef pair<int,int> PII;
const int N = 110;
int n,m;
int g[N][N];     // 存的地图
int d[N][N];     // 到起点的距离
PII q[N * N];    // 定义的队列
PII Prev[N][N];
int bfs(){
    int hh=0, tt=0;
    q[0] = {0,0};
    int dx[4] = {-1,0,1,0}, dy[4] = {0,1,0,-1};
  
    memset(d,-1,sizeof d);
    d[0][0] = 0;
    while(hh <= tt){
        auto t = q[hh++];
    
        for(int i=0;i<4;i++){
            int x = t.first + dx[i];
            int y = t.second + dy[i];
            if(x>=0 && x<n && y>=0 && y<m && g[x][y]==0 && d[x][y]==-1){
                d[x][y] = d[t.first][t.second] + 1;
                Prev[x][y] = t;
                q[++tt] = {x,y};
            }
        }
    }
    // int x = n-1,y = m-1;
    // while(x || y){
    //     cout<<x<<" "<<y<<endl;
    //     auto t = Prev[x][y];
    //     x = t.first,y=t.second;
    // }
    return d[n-1][m-1];
}

int main(){
    cin>>n>>m;
    for(int i=0;i<n;i++)
        for(int j=0;j<m;j++)
            cin>>g[i][j];
  
    cout<<bfs()<<endl;
    return 0;
}

八数码问题

#include<bits/stdc++.h>
using namespace std;

int bfs(string start){
    string end = "12345678x";
    queue<string> q;
    unordered_map<string,int> d;
  
    q.push(start);
    d[start] = 0;
  
    int dx[4] = {1, -1, 0, 0}, dy[4] = {0, 0, 1, -1};
    while(q.size()){
        auto t = q.front();
        q.pop();
        int distance = d[t];
        if(t==end) return distance;
        int k = t.find('x');
        int x = k / 3, y = k % 3;
    
        for(int i=0;i<4;i++){
            int a = x + dx[i];
            int b = y + dy[i];
            if(a>=0&&a<3&&b>=0&&b<3){
                swap(t[k], t[a * 3 + b]);
                if(!d.count(t)){
                    d[t] = distance + 1;
                    q.push(t);
                }
                swap(t[k], t[a * 3 + b]);
            }
        }
    }
    return -1;
}

int main(){
    string c,start;
    for(int i=0;i<9;i++){
        cin >> c;
        start += c;
    }
    cout << bfs(start) << endl;
    return 0;
}

DFS && 哈希函数